Preocupările pentru a găsi modele matematice care să descrie evoluția în timp a bolilor infecțioase datează de cel puțin câteva sute de ani. Primul model a fost obținut în 1760 de D. Bernoulli [1] care descrie evoluția variolei. Un pas important în obținerea unui model dinamic a fost făcut în 1911 de doctorul R. Ross [7], lauret al Premiului Nobel pentru medicină în 1902 pentru contribuțiile sale la studiul și înțelegera malariei, care a avut curajul să formalizeze descoperirile sale și din punct de vedere matematic. Mai sunt apoi modele empirice, făcute prin colectarea informațiilor despre epidemii care au avut loc de-a lungul timpului în diverse zone. Modelul matematic cel mai vechi, și cel mai utilizat, a fost obținut de către W.O. Kermack and A.G. McKendrick [5] în 1927 și, de atunci, nu a încetat sa-și dovedească utilitatea. O prezentare foarte cuprinzătoare și pertinentă a modelelor matematice din epidemiologie este cea a lui H.W. Hethcote [4].
Sunt două tipuri de modele care sunt utilizate în epidemiologie, cele matematice, cu preponderență dinamice, și cele statistice. Aceste două tipuri de model sunt într-o relație simbiotică: modelele matematice constituie osatura oricărei abordări științifice a bolilor transmisibile iar cele statistice constituie musculatura acestor abordări, cele care fac legătura cu cazurile reale. În al doilea rând, având în vedere că modelele sunt foarte generale, ele sunt aplicabile nu numai bolilor umane ci și celor din lumea animală, în ecosisteme. Dar, deși aceste modele par foarte simple, din punct de vedere matematic ele pun niște probleme care nu au întotdeauna o soluție simplă, sau chiar sunt probleme care încă nu au un răspuns satisfăcător. Modelul SIR, pe care doresc să-l prezint, se studiază de obicei la cursul de sisteme dinamice, vezi M. Hirsh, S. Smale, R.L. Devaney [5], dar importanța lui transcende cu mult aspectul didactic. Evoluțiile din ultimele două luni ale propagării virozei provocate de virusul COVID-19 nu sunt chiar o surpriză pentru cei care încearcă să ințeleagă această lume dintr-un punct de vedere rațional.
Supriza mare a venit însă din partea unor politicieni care, deși aveau rapoartele epidemiologilor din agențiile naționale pentru controlul bolilor contagioase, au considerat că este preferabil fie să ignore aceste informații fie să le bagatelizeze. Experiența spune că, atunci când ai la îndemână un model matematic pentru un anumit fenomen, este recomandat sa ții cont de el fiindcă, altfel, realitatea te lovește în față atunci când te aștepți mai puțin. Din păcate, lucrul acesta s-a întâmplat atât în Europa, leagănul civilizației moderne care a pus rațiunea ca fundament și care își datorează avansul exact dezvoltării științelor și a matematicii, cât și în Statele Unite ale Americii, sora mai mică și mai vitează. Dar, viața este plină de surprize.
O schimbare majoră de abordare din partea politicienilor a avut loc pe la jumătatea lunii martie când a fost publicat primul raport al ,,Imperial College COVID-19 Response Team” [2] care, pe baza prezentării unei analize obținută cu ajutorul modelelor cunoscute, a prezis cel puțin câteva sute de mii de victime numai în Marea Britanie, în caz că nu se iau măsuri de distanțare socială și în lipsa unor instrumente farmaceutice de tip medicamente antivirale sau vaccinuri. Confruntați și cu realitatea din Italia, politicienii au fost nevoiți să-și schimbe radical abordarea, în cele din urmă. La final, după numărătoarea victimelor și a pagubelor produse, poate că se vor trage și niște concluzii și se vor atribui responsabilitățile.
Scopul meu este să explic, pentru o audiență foarte largă, ce este modelul SIR și cum poate fi folosit pentru a înțelege ce anume se întâmplă în aceste zile nebune, cu atmosferă desprinsă din filmele SF. Forma de prezentare este ceva mai formalizată, prin comparație cu articolele de pe această platformă, cu câteva formule matematice dar care nu depășesc nivelul de cunoștințe necesare pentru a obține o diplomă de bacalaureat, și câteva grafice pentru câteva simulări.
Modele cu Compartimente. În epidemiologie se utilizează de mult timp niște modele dinamice pentru evoluția bolilor contagioase, numite modele cu compartimente. Se consideră o populație (o localitate, o aglomerare de localități, un județ, o țară, etc.) stabilă cu N locuitori (se ignoră nașterile, decesele și migrările), relativ omogenă, în care interacțiunile dintre locuitori au loc în mod continuu. Această populație se împarte în compartimente notate cu M, E, S, I, R, cu următoarele definiții:
M este numărul bebelușilor care au imunitate pasivă, moștenită în mod natural de la mamă, dar care durează un număr limitat de luni.
S este numărul de indivizi care sunt susceptibili de a fi infectați, care nu au imunitate.
E este numărul indivizilor care sunt în perioada lantentă de infectare dar care încă nu sunt contagioși.
I este numărul indivizilor care sunt infectați și care sunt contagioși, adică îi pot infecta pe oricare dintre indivizii din compartimentul S cu care intră în contact.
R este numărul indivizilor care au fost infectați dar care, fie s-au vindecat căpătând imunitate și deci nu mai sunt contagioși, fie au decedat.
Transferul dintre compartimente poate avea loc doar în urmatoarele moduri:
– din compartimentul M se poate trece doar în compartimentul S după un interval de timp relativ constant;
– din compartimentul S se poate trece doar în compartimentul E pentru un interval de timp relativ constant;
– din compartimentul E se poate trece doar în compartimenul I al celor infectați și contagioși;
– din compartimenul I se poate trece doar în compartimentul R fie prin vindecare și căpătarea unei imunități naturale fie prin deces.
|
M ® |
S ® |
E ® |
I ® |
R |
Modelul cu compartimente descris se numește MSEIR și este cel mai complex.
Modelul SIR. W.O. Kermack și A.G. McKendrick (1927) au publicat rezultatele obținute pe un model dinamic simplificat SIR cu doar trei compartimente, S, I, și R, numit și modelul clasic pentru epidemie, în care au loc doar următoarele transferuri:
– din compartimentul S se poate trece doar în compartimentul I;
– din compartimentul I se poate trece doar în compartimentul R.
|
S ® |
I ® |
R |
Modelul dinamic SIR se obține făcând mai departe următoarele presupuneri:
– sistemul dinamic evoluează în timp continuu iar funcțiile S, I, și R sunt funcții de timp S(t), I(t), R(t) netede, în limbaj matematic având seminificația că sunt diferențiabile de orice ordin (indefinit diferențiabile) pe intervalul de timp [0, ∞).
– β (beta) este parametrul care controlează transferul între compartimentele S și I, cu semnificația că reprezintă numărul mediu de contacte suficient pentru infectare, pe unitatea de timp;
– γ (gama) este rata de transfer între compartimentul I și compartimentul R, care cuprinde atât rata de vindecare cât și rata de deces, fără a face diferențiere între acestea două, cu semnificația că 1/γ este intervalul de timp în care un individ rămâne infectat.
Din prespunerea că numărul de indivizi rămâne constant rezultă că S(t)+I(t)+R(t)=N la orice moment t. În cele ce urmeză folosim notațiile pentru derivata unei funcții g atât în forma Leibniz dg/dt cât și în forma Newton g’. Din prespunerile modelului și definițiile parametrilor β și γ rezultă următorul sistem de ecuații diferențiale de ordin unu:
dS(t)/dt = – β S(t) I(t)/N
dI(t)/dt = β S(t) I(t)/N – γ I(t)
dR(t)/dt = γ I(t)
De fapt, se consideră normalizările celor trei funcții S, I, R definite astfel: s(t)=S(t)/N, i(t)=I(t)/N, r(t)=R(t)/N, unde N este numărul total de indivizi, iar relația dintre aceste funcții normalizate devine condiția s(t)+i(t)+r(t)=1, la orice moment t. Sistemul diferențial devine:
ds(t)/dt = – β s(t) i(t)
di(t)/dt = β s(t) i(t) – γ i(t)
dr(t)/dt = γ i(t)
Sistemul diferențial SIR este de obicei însoțit de datele inițiale s(0)=s0, i(0)=i0, r(0)=r0, care descriu sistemul la momentul de pornire, caz în care vorbim despre o problemă cu valori inițiale (PVI). Cele trei ecuații nu sunt independente, de exemplu a treia se obține din primele două ținând cont că din condiția s(t)+i(t)+r(t)=1 se obține s'(t)+i'(t)+r'(t)=0.
Bifurcație – Epidemie sau Nu. Sistemul SIR este neliniar. Nu se cunosc forme explicite analitice ale soluțiilor sistemului SIR, deși sunt cunoscute forme parametrice, soluții prin serii de puteri, ș.a., cf. T. Harko, F.S.N. Lobo, M.K. Mak [3]. Evoluția sistemului dinamic SIR, deci aspectul calitativ, este diferită în funcție de așa numitul număr de reproducere r (ro) definit prin r = s0b/g. Numărul de reproducere este important fiindcă ne arată cum va evolua răspândirea bolii din punct de vedere epidemiologic: conform unui rezultat arhicunoscut de analiză matematică care spune că semnul derivatei unei funcții controlează caracterul monoton (creștere/descreștere) al funcției, iar semnul derivatei funcției i(t) se poate observa din a doua ecuație a sistemului SIR, ceea ce ne conduce la a spune când avem β s(t) – γ pozitiv sau negativ.
Un sistem dinamic se spune că are o bifurcație dacă la o schimbare mică a unui anumit parametru (parametrul de bifurcație) are loc o schimbare a sistemului esențială din punct de vedere calitativ. În cazul sistemului dinamic SIR, parametrul de bifurcație este numărul de reproducere r iar bifurcația are loc pentru r aproape de valoarea 1, în sensul următor:
– dacă r>1 atunci funcția i(t), care descrie numărul de indivizi infectați, crește până la o valoare maximă după care începe să scadă și spunem că are loc o epidemie.
– dacă r<1 atunci funcția i(t) descrește de la valoarea inițială i(0) până la valori apropiate de zero și în acest caz nu are loc o epidemie.
Discretizare Euler. În absența unei soluții explicite și pentru a avea o perspectivă asupra a ce se poate spune din punct de vedere calitativ despre modelul SIR, de obicei se face o discretizare de tip Euler, care înseamnă că facem o eșantionare a intervalului de timp [0, T] în intervale de timp de lungimi egale DT, iar în loc de funcții avem șiruri (sn), (in), (rn), cu date inițiale s(0)=s0, i(0)=i0, r(0)=r0. Se obține în acest fel un sistem de relații de recurență, numit sistem cu diferențe, în loc de sistem de ecuații diferențiale.
Descriem pe scurt metoda lui Euler de discretizare a ecuațiilor diferențiale de ordin unu. Se consideră o funcție y=y(t), diferențiabilă pe un interval [0, T], unde T poate fi finit sau infinit, pe care se face o eșantionare în intervale de timp de lungimi egale DT, producând șirul (yn)n definit prin yn=y(n), cu relația de recurență
yn=yn-1+pantan-1 × DT
unde pantan-1 are semnificația discretă a derivatei. În acest fel, forma discretizată a modelului SIR devine:
sn = sn-1 – b sn-1 × in-1 × DT
in = in-1 + b sn-1 × i × DT – g in-1 × DT
rn = rn-1 + g in-1 × DT
Avantajul sistemului cu diferențe este că putem avea foarte rapid soluții numerice, simulări, comparări cu date reale, etc.
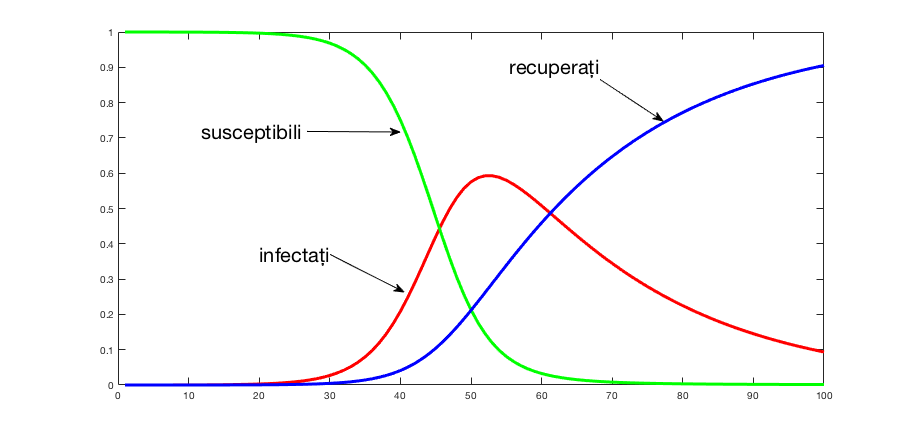
Simulări. Am făcut câteva programe în MATLAB utilizând discretizarea Euler a modelului SIR. Prima simulare este pentru graficele celor trei funcții, susceptibili, infectați, și recuperați, pentru un interval de timp de 100 de zile, cu valori raportate zilnic. În Figura 1 avem o simulare cu b=0,3, g= 1/23, i(0)=1/27000, r(0)=0, s(t) linia verde, r(t) linia albastră, i(t) linia roșie.
Figura 1.
A doua simulare prezintă evoluția numărului de indivizi infectați pentru parametrii g= 1/23, i(0)=0,1, r(0)=0,03, pentru un interval de timp de 100 de zile, cu valori raportate zilnic, și variind parametrul b cu valori între 0,0025 și 0,1 cu intervalul de eșantionare de 0,0025. Bifurcația, schimbarea evoluției funcției i(t), din descreștere permanentă în creștere urmată de descreștere, are loc pentru b = 0,04349, respectiv atunci când numărul de reproducere r=s0b/g din subunitar devine supraunitar, vezi Figura 2.
Figura 2.
Am făcut o a treia simulare cu următorul scenariu: are loc o epidemie cu numărul de reproducere r>1, iar după un interval de timp, prin măsuri de distanțare socială, de exemplu, acest număr devine subunitar, apoi măsurile de distanțare socială se relaxează, ceea ce face ca în scurt timp r devine iarăși supraunitar, și scenariul se repetă tot așa de căteva ori. În acest caz, numărul indivizilor infectați are perioade de creștere și perioade de descreștere, urmând schimbările coeficientului b cu o anumită inerție. În Figura 3 se observă schimbările evoluției numărului de indivizi infectați ca urmare a variației coeficientului b în intervalul 0,4 și 0,1 pentru intervale de timp de câte 30 de zile.
Figura 3.
Câteva concluzii. Modelul dinamic SIR ne oferă posibilitatea să înțelegem cam ce anume se poate întâmpla cu evoluția unei epidemii și cam la ce anume să ne așteptăm. Numărul de reproducere r ne spune dacă avem o epidemie sau nu și avem doi parametrii b și g cu care se poate lucra pentru limitarea epidemiei. Parametrul b ține de organizare socială și instituții publice pe când parametrul g ține de aspecte medicale. În absența remediilor medicale de tip medicamente antivirale și vaccinuri ne rămâne doar să încercăm să micșorăm parametrul b prin măsurile care se iau în prezent. Altfel, propagarea virozei decurge urmând modelul iar consecințele sunt greu de evaluat. În realitate, atât b cât și g nu sunt constante ci variază în timp, însă aspectul general al răspândirii virozei se poate obține chiar și în acest caz utilizând discretizarea modelului SIR. Speranța vine din zona biologiei celulare și a laboaratoarelor de cercetare farmaceutică fiindcă, altfel, mai devreme sau mai târziu ne vom infecta cu toții.
Mulțumiri doamnei lector doctor Eliza Gheorghe, de la Departamentul de Relații Internaționale al Universității Bilkent, pentru observații foarte utile asupra unei versiuni preliminare a acestei note.
Referințe.
[1] D. Bernoulli, Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir, Mémoires de Mathématiques et de Physique, Académie Royale des Sciences, Paris, 1760, pp. 1-45.
[2] Imperial College COVID-19 Response Team, http://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/
[3] T. Harko, F.S.N. Lobo, M.K. Mak, Exact analytical solutions of the susceptible-infected-recovered (SIR) epidemic model and of the SIR model with equal death and birth rates, Appl. Math. Comput. 236(2014), 184-194.
[4] H.W. Hethcote, The mathematics of infectious disease, SIAM Review, Vol. 42, No. 4 (2000), 599-653.
[5] M. Hirsh, S. Smale, R.L. Devaney, Differential Equations, Dynamical Systems, and an Introduction to Chaos, 2nd Edition, Elsevier, Amsterdam 2004.
[6] W.O. Kermack and A.G. McKendrick, Contributions to the mathematical theory of epidemics, Part 1, Proc. Roy. Soc. London Ser. A, 115(1927), 700-721.
[7] R. Ross, The Prevention of Malaria, Murray, London 1911.








 Aikido cu mintea si corpul coordonate. Invatati cum sa va relaxati si cum sa va pastrati calmul in conditii de stress.
Aikido cu mintea si corpul coordonate. Invatati cum sa va relaxati si cum sa va pastrati calmul in conditii de stress. 
Cineva a făcut un calculator pe baza modelului ăsta, aici: http://gabgoh.github.io/COVID/index.html
Problema constă în a găsi parametrii corecți….
Modelul la care faceți referire este puțin mai complex. Intenția mea a fost să explic principiile în forma cea mai simplă. Agențiile mari care se ocupă de controlul bolilor infecțioase folosesc modele și mai complexe care combină modelul dinamic cu cel statistic, fiindcă sunt interesați de estimări în timp real și pe baza cărora se pot lua hotărâri cât de repede posibil.
Excelent material: scurt, cuprinzator, la obiect.
Pacat ca, tocmai in aceste zile, lumea sa inghesuie sa-i citeasca pe aburitorii de serviciu, la care numarul de vizualizari e direct proportional cu numarul si anvergura prapastiilor insirate.
Cam asta este ideea: având în vedere că modelele matematice sunt cunoscute de atâta timp, este încă surprinzător ca oameni care au trecut prin școală încă pot marșa la argumente fanteziste.
Din pacate la fundamentul civilizatiei moderne nu e doar ratiunea, ci si o doza periculoasa de mindrie, chiar aroganta si mult confort, chiar individual ne complacem in laissez fire de zi cu zi (nu neaparat ala economic). Multe tari au ignorat pericolul cind pericolul era deja in interiorul lor. Au luat masuri usoare, plapinde. Au pierdut si inca pierd enorm.
Si ca exemplu, nici noi nu am luat masuri devreme, ci atunci cind pericolul era unul clar. Daca masurile actuale erau luate mai devreme se trata o epidemie usoara si poate revenirea ar fi durat mai putin. Dar a existat o anumita teama de a impune masuri mai dure devreme.
Este într-adevăr uimitor. În urmă cu zece ani am urmărit o prezentare în cadrul unui seminar din departament al unui matematician care lucra la CDC, centrul pentru controlul bolilor din Statele Unite, și care a vorbit despre modelele matematice cu care lucrează agenția, printre care și modelul SIR. Politicienii au rapoarte foarte detaliate de la echipele acestor agenții și ceea ce este de mirare este că le ignoră până când este prea târziu. În cazul COVID-19, se știa încă de la începutul anului că numarul de reproducere este mare.
Raspandirea este mare si atunci care sunt masurile care ar trebui luate?
faptul ca covid-19 se tine mai mult pe suprafete decat alti virusi poate conduce la o crestere a gradului de raspundire?
Cum explicati diferentele mari ale modului in care a evolutat situatia in Italia/Franta fata de Germania/Olanda?
Care este baza minima de seturi de date de la care poti sa construiesti un model ce simuleaza relativ apropiat de realitatea din teren?
După cum am spus, modelul SIR se aplică pentru o populație bine delimitată, cu un grad de omogenitate mare. Aplicarea la nivel de țară în forma aceasta nu se face așa, ci printr-o rafinare, cu mai multe compartimente și cu componente statistice la zi. Agențiile naționale, sau echipe multidisciplinare cum este Imperial College COVID-19 Response Team, utilizează, pe scheletul modelului SIR, modele mult mai complexe și pe baza acestora emit predicții. Am și eu un model puțin mai complex pe care îl utilizez pentru uzul personal dar nu îmi permit să ies în spațiul public cu predicții fiindcă datele pe care le am sunt parțiale, multe dintre ele puțin credibile, și deci predicțiile pot fi foarte departe de realitate. În componenta statistică nu mai este vorba de matematică ci mai degrabă de meșteșug, o zonă în care nici nu mă simt confortabil și pe care nici nu o prea agreez.
Ce fel de măsuri ar trebui să fie luate, ce se poate face pe partea medicală, sunt întrebări care depășesc aria mea de competență și nu mă aventurez să fac afirmații hazardate. La clasă, când se fac aplicații pe acest model, se poate face o analiză post factum, pentru epidemii trecute, pentru care informația există și a fost bine verificată. De exemplu, pentru gripa Hong Kong din New York din 2009, datele există și se poate explica foarte mult referitor la viabiliatea modelului.
Parerea mea este ca nu masurile dure ne-au lipsit ci practic nu ne-am pregatit
– cu echipamente de protectie: masti, costume,
– teste si aparate de testat,
– ventialtoare, paturi in sectiile de ATI
– medicamente care pot ajuta vindecarea
si mai ales nu am instructat cadrele medicale.
Dpmdv masurile stricte de limitarea a libertatilor au fost prea agresive – aproape nemeritat de agresive la adresa populatiei – ele trebuiau sa tinteasca in alta parte – gtranzitarii si diasporenii -si poate ar fi trebuit sa imbrace alta forma –
Nici acum in ceasul 25 nu imbunatatim protocoalele si culmea este ca insa sunt cadre medicale care se obraznicesc atunci cand nimic nu justifica aroganta lor.
In Ro s-a marsat prea mult pe reducerea raspandirii prin limitarea interactiunilor umane – izolarea cu si fara motiv – in speranta ca nu vor aparea focare de infectii –
dar uite ca ele au aparut imbolnavirile fie dupa oarece calatorii ale bastinasilor in zonele externe de puternic expuse din afara tarii, fie prin nerespectarea unor masuri absolut obligatorii de protectie si,sau izolare personala.
O parere.
Felicitari pentru articol.
Mulțumesc. Am apreciat întotdeauna articolele dumneavoastră pe această platformă.
Toate bune si frumoase, chiar si eu am priceput. Problema e de unde iei datele de intrare. De ex. se spune ca nr real al celor infectati e de sase ori mai mare decit cel certificat-oficial. https://www.t-online.de/nachrichten/panorama/id_87634848/corona-krise-nur-jede-sechste-infektion-in-deutschland-wird-erkannt.html
De asemenea nici celelelate date nu sunt clare, e si logic odata ce nu stii cit sunt infectati nu poti stii citi sunt vindecati din ei.
O intrebare ar fi „S” se refera la totalul populatiei, se imagineaza ca toata populatia ar fi susceptibila de infectie? Exista in aceste modele si indivizi care nu se infecteaza, pur si simplu?
Ceea ce am prezentat eu este modelul cel mai simplu, de manual, care poate fi înțeles de oricine care are un bagaj minimal de matematică (de liceu). Sunt modele mult mai sofisticate, care au fie mai multe compartimente, fie au componente statistice. Pe baza informațiilor acumulate în epidemii trecute, se poate estima destul de acceptabil cam care ar fi aceste numere. Sunt agenții care estimează numarul celor infectați cam de zece or numarul celor depistați prin testare.
Chiar dacă nu avem informații despre numărul celor infectați și al celor susceptibili, ceea ce se face în practică este un model probabilist, în care în fiecare zi îți recalculezi coeficienții beta și gama, pe baza informațiilor din trecutul apropiat.
Din punct de vedere procedural, este foarte asemănător cu metodele disponbilie cu cunoștințele actuale care se utilizează în prognoza meteo. Nu știe nimeni cum se pot rezolva analitic ecuațiile Navier-Stokes, care modelează dinamica fluidelor, deci atmosfera terestră, și atunci în fiecare zi se recalculează parametrii având datele meteo de ieri. Puteți face următorul experiment: urmăriți prognoza meteo pentru următoarele 15 zile și comparați cum se schimbă prognoza în timp ce vă apropiați de ziua inițial a cincisprezecea, prin ajustarea parametrilor. Prognoza pentru următoarele cinci zile este excelentă, pentru intervale de timp mai mari este mai puțin corectă, dar este corectată în fiecare zi.
Ar fi cateva probleme:
1. Acei care ne conduc, formatorii de opinie, dar si multi care nu au mai trecut pe la scoala de mult timp (inclusiv medici), uita ce inseamna rigoarea matematica si stiintifica, cifrele si teoriile nu le spun nimic. Pentru multi calculatorul e facebook. Deciziile in mare majoritate se iau dupa ureche. Eu as zice ca orice decizie ar trebui sa se ia si dupa niste masuratori, modele reale.
2. Am auzit o explicatie de ce au reactionat tarziu chiar daca au fost avertizati din timp. Zice ca in democratie un politician nu poate lua asa decizii de capul lui, in democratie electoratul trebuie sa ceara sa tipe si sa insiste ca ei sa se miste. Democratiile intotdeauna iau deciziile mai greu, cu intarziere.
Grigore Moisil, matematician cu o personalitate foarte puternică, a lăsat multe fraze memorabile: ,,Azi facem matematica ce va fi folosită mâine şi mai ales poimâine. Că dacă n-am face-o azi, poimâine ar trebui s-o importăm.” Modelul SIR este disponibil de aproapte o sută de ani.
Astăzi mi-a trimis o prietenă o știre foarte interesantă. O cercetătoare biolog a fost întrebată când vor fi disponibile medicamentele antivirale. Răspunsul a fost memorabil: un cercetător biolog este plătit cu 1800 de euro pe lună. Voi îi plătiți pe fotbaliști cu milioane de euro. De ce nu-i întrebați pe Messi și Ronaldo de medicamente antivirale?
” Surpriza mare a venit insa din partea unor politicieni …”
Pentru mine surpriza mare a fost ca politicienii in cauza – Donald & Boris – au ignorat – in primele pozitionari – asteptarile publicului ( lor ) .
Pozitia pe care au adoptat-o in prima faza – ” pragmatica ” / ” rationala ” – pare sa indice ca marii barbati D & B se considera ” oameni de stat ” ( politicieni capabili sa impuna publicului ideile lor ) .
Ceea ce nu prea are vreo legatura cu Realitatea , Donald & Boris fiind simpli ” lideri politici ” ( politicieni care raspund dorintelor / asteptarilor publicului lor ) .
Din punct de vedere politic , era o problema simpla / elementara .
Si a durat mai bine de o saptamana sa se trezeasca / sa fie treziti …
Nu cred ca vor avea de suportat costuri politice .
Oamenii nu prea inteleg .
Si uita repede .
Din ultimele informații, domnul Boris Johnson plătește un preț (la modul personal) destul de mare.
Nu stiu …
Parca nu as exclude posibilitatea ca asta sa fie o mica sceneta …
Cu scopul de a-l scoate pe Boris de pe radar , a-l transforma in victima , a face uitata abordarea initiala si responsabilitatea pentru evolutia ulterioara …
Boris are antecedente ( dovedite ) de mare mincinos iar consilierul sau principal Dominic are o buna reputatie de manipulator …
O sa ma lamuresc functie de momentul pe care Boris il va alege ca sa-si faca reintrarea in scena ( dupa depasirea varfului , ca sa dea el vestea cea buna , as zice ) …
Intre timp , Donald sugereaza ca Administratia SUA nu putea opri zborurile din China pana cand OMS nu se pronunta daca e sau nu pandemie …
Adanc …
Amintiri răzlețe…Am aflat despre modelul ȘIR de la regretatul prof. de ftiziologie Leon Daniello de la Universitatea de Medicina Cluj in anul 1967. Dansul era stupefiat de numărul mare de cazuri de tuberculoza detectate in rândul elevilor clujeni in urma unei campanii de injectare cu tuberculina. La scurt timp s-a terminat tuberculina iar profesorul dorea sa sensibilizeze CC al PCR pentru continarea campaniei, temându-se de o epidemie. Având datele dansului împreuna cu doi asistenți ai săi și un coleg statistician cu ajutorul modelului ȘIR am reușit sa-i prezentam o prognoza care l-a cam speriat. Am reușit sa prezentam o comunicare la un Simpozion de statistica la Brașov dar aceasta n-a mai.aparut in Lucrările simpozionului. Cred ca s-a speriat și…Partidul. Se pare c-am pierdut lucrarea dar numele Kermack și McKendrick nu se uita!
Da, atunci când politica se face împotriva intereselor generale cam asta se întâmplă.
Frumos articol si bine venit data fiind situatia actuala.
Mulțumesc.
Frumos articol!un cod în Matlab pentru simularea acestuia se poate?